
Figure 0. The Mandelbrot set.
Home > Essays > An explanation of the Mandelbrot set for artists

You have seen this image before, or some variation of it. You might also know that it's called the Mandelbrot set and that Benoît Mandelbrot was the first to thoroughly study it in the late 1970s, though the image Mandelbrot first looked at might have looked more like this:

You might also know that it has something to do with math. You might even know that it is an example of a fractal.
But the problem with most explanations of the Mandelbrot set is that they seem to require advanced knowledge of calculus, plus the whole Greek alphabet. It is a very interesting image, and some artists are of course interested in incorporating it into their artwork.
For this reason, I feel that it's necessary to have some explanation of it that is accessible to artists, who can be counted on to at least have a decent grasp of practical arithmetic and very basic algebra.
The two key mathematical concepts to understand here are iteration and "complex" numbers. As iteration seems to be the easier concept to explain, that's what I will start with.
Iteration is just the repeated application of a function, at each step after the initial step using the result of the previous step as the input. Depending on the function and the initial value, iteration can produce an infinite sequence of distinct numbers, or it can repeat the same numbers over and over again in some pattern.
The iterated function that is of special interest to us here is this: multiply a number by itself and add a constant value. Algebraically, we can express this as z2 + c. Here, z2 is z multiplied by itself and c is the constant value (if you remember your high school algebra, the choice of z rather than x may seem strange; it will be explained later on).
In my opinion, the best choice for the starting value is z = c. However, technically, the correct choice is z = 0. But since 02 = 0, all this does is add an unnecessary extra step to the calculations. It's not a big deal for our fast modern computers, but in 1995, details such as these made the difference between an image showing up on the screen in a matter of minutes rather than a matter of hours.
Let's try c = 2. The function is then z2 + 2. The first iteration gives 22 + 2 = 6. The next iteration gives 62 + 2 = 38. And the next: 382 + 2 = 1446. Then 2090918, 4371938082726, 19113842599189892819591078, ... If you're following along with a pocket calculator, you've probably already gotten an overflow error.
You can go a little farther with a scientific calculator, and farther still on a computer with a program like Maple or Mathematica. But you don't need a bigger calculator to see that these numbers just keep on getting bigger and bigger. A mathematician might say that the iteration escapes to positive infinity.
Now let's try c = −2. The function is then z2 − 2. The first iteration gives (−2)2 − 2 = 2 (remember that a negative number times a negative number is a positive number). The next iteration gives 22 − 2 = 2 again. The iteration is stuck on 2. A mathematician might say that the iteration attains a stable orbit. A regular person might say the iteration attains a boring orbit.
We can express this concept of iteration a little more algebraically by using subscripts to keep track of how many iterations have been performed. Write z0 = 0, and, for n a positive integer, zn = (zn − 1)2 + c.
Using this notation with subscripts, we have z0 = 0 and z1 = c. Then z2 is the first iteration for which we don't automatically know the value. So in the case of c = −2, we have z0 = 0, z1 = −2, z2 = 2, z3 = 2, z4 = 2, z5 = 2, etc.
| n | zn |
|---|---|
| 1 | 0.25000000 |
| 2 | 0.31250000 |
| 3 | 0.34765625 |
| 4 | 0.37086487 |
| 5 | 0.38754075 |
| 6 | 0.40018783 |
| 7 | 0.41015030 |
| 8 | 0.41822327 |
| 9 | 0.42491070 |
| 10 | 0.43054911 |
| ... | ... |
| 3991 | 0.49975007 |
| 3992 | 0.49975013 |
| 3993 | 0.49975019 |
| 3994 | 0.49975025 |
| 3995 | 0.49975032 |
| 3996 | 0.49975038 |
| 3997 | 0.49975044 |
| 3998 | 0.49975050 |
| 3999 | 0.49975057 |
| 4000 | 0.49975063 |
Escaping to infinity or getting stuck on a particular number aren't the only two possibilities of iteration. Consider c = 1/4 = 0.25, so the function is then z2 + 1/4. The first iteration gives us 5/16 = 0.3125. Then 89/256 = 0.34765625, 24305/65536 = 0.3708648681640625, ... This is not going to escape to infinity.
It might get stuck on 1/2 = 0.5. After all, 1/2 times 1/2 equals 1/4, and when you add 1/4 to that you're back to 1/2. That's actually not what happens either. After a thousand iterations, we have approximately 0.49900959. After two thousand iterations, we have approximately 0.49950258. And after four thousand iterations, approximately 0.49975063.
Those numbers are from a spreadsheet program with a display precision of eight decimal digits (I can set more precision, if I want, but there are limitations). Carried far enough, this iterated function will take the computer to a point where the computer can't distinguish between 1/2 and the actual number. But with infinite precision, the iteration gets "arbitrarily" close to 1/2 without ever actually reaching it.
We can still view this as an either-or: either the iterated function escapes to infinity or it doesn't. Take the real number line, with c = 0 at the center, painted in white, and change to black the pixels corresponding to c such that the iterated function z2 + c does not escape to infinity.
So as to avoid getting the computer stuck in an infinite loop, we'll program the computer to keep track of how many steps in the iteration it has performed and instruct it to stop at a certain threshold and move on to the next point if it does not find evidence that the iteration escapes to infinity. Also, we'll instruct it to assume that the iteration has escaped to infinity if a step results in a value greater than 2.
And so, by this process, we obtain a black line that goes from c = −2 to c = 1/4.

Not the most exciting diagram. But we haven't yet ventured out to a wider universe of numbers.
A "complex" number has a "real" part and an "imaginary" part. This whole terminology is unfortunate because it suggests that complex numbers are too complicated to be of any use, and that imaginary numbers have no basis in reality.
But at least it allows me to draw a parallel to Impressionism in the visual arts. The term started out as an insult, but now critics and collectors have come to appreciate Impressionism, while mathematicians, scientists and engineers have recognized the usefulness of imaginary and complex numbers.
The real part of a complex number is a real number, and the imaginary part of a complex number is an imaginary number.
We can use real numbers to measure most solids, liquids and gases, which is what helps give these numbers a sense of reality. What the imaginary numbers measure are things which we have only recently come to understand, or are still struggling to understand, things like electricity and quantum particles.
However, the context in which mathematicians first encountered imaginary numbers was in algebra.
A simple equation like x2 − 1 = 0 has one obvious solution and one less obvious solution that should still be easy to come by. But if you have any difficulty whatsoever with this sample equation, you can make things easier by adding 1 to both sides, thus going from x2 − 1 + 1 = 0 + 1 to just x2 = 1.
Then the obvious solution is x = 1. The less obvious solution is x = −1 (remember that a negative number times a negative number is a positive number). This is not the place to expound on the fundamental theorem of algebra, but there is one corollary of it that is of relevance here:
If y is a positive real number, then the equation x2 = y has two solutions, one positive (called the "principal" square root), the other negative.
Now let's look at a very similar equation: x2 + 1 = 0, which we simplify by subtracting 1 from both sides to obtain x2 = −1. Your calculator is not going to self-destruct because you ask it to compute the square root of a negative real number, but it will lock up in an error state and you'll have to press C or CE to do anything else.
Confronted by equations of this kind long ago, one mathematician had the bright idea of assuming that a solution does exist and seeing what happens. Let's call this solution i. All we know about i at the moment is that i2 = −1. The solution to x2 + 1 = 0 is x = i.
That mathematician's contemporaries must have thought this was some kind of trickery or sophistry. We can imagine that an equation has as many solutions as we like, but that doesn't change the reality of an equation that has no real solutions, they would say.
It was a slow process to realize that imaginary numbers do have a basis in reality and that they are part of a consistent number system, but the terminology stuck.
If a positive real number has two square roots, does a negative real number also have two square roots? If we multiply i by −1, we get −i. Then (−i)2 = (−1 × i)(−1 × i) = (−1)2 (−i)2 = 1 × −1 = −1. Hence x = −i is another solution to the equation.
Take a real number b and multiply it by i to get bi (in general, mathematicians prefer not to use the multiplication sign unless it's absolutely necessary). That's all an imaginary number is: a real number multiplied by i.
If y is a positive real number, then the equation x2 = y has two solutions, one is √y and the other is −√y. And the equation x2 = −y also has two solutions, one is i√y and the other is −i√y.
I'm not going to go in-depth about the square roots of nonzero imaginary numbers. Suffice it to say that they are complex numbers, i.e., numbers with a nonzero real part and a nonzero imaginary part. For example, the square root of i is approximately is 0.7071 + 0.7071i.
It's more important now to go over the arithmetic of complex numbers. If x and y are real numbers, yi is an imaginary number and x + yi is a complex number.
Let's say v + wi is another complex number. Then (x + yi) + (v + wi) = (x + v) + (y + w)i. For example, (−3 + i) + (7 + 2i) = 4 + 3i. We can add a purely real or purely imaginary number to a complex number, just so long as we take care to put in zeroes at the appropriate spots so as to properly line up the real parts and the imaginary parts.
To multiply complex numbers is not complicated at all. The FOIL mnemonic you might remember from high school is helpful here, but it winds up being a little more like FLOI: (v + wi)(x + yi) = (vx − wy) + (vy + wx)i. For example, (−3 + i)(7 + 2i) = (−21 − 2) + (7 − 6)i = −23 + i.
As with the formula for the addition of complex numbers, the formula for the multiplication of complex numbers can also be used if one of the multiplicands is a purely real or purely imaginary number, so long as we take care to put in zeroes at the appropriate spots.
If the real number line is horizontal and includes 0, and the imaginary number line also includes 0, it makes sense to make the imaginary number line vertical and attach it to the real number line so that they're perpendicular and their intersection is at 0.
This is the basis for a diagram of the complex plane. Any complex number can be located in the complex plane by first identifying the real part on the real number axis and the imaginary part on the imaginary number axis and then drawing lines into the appropriate quadrant of the complex plane. Where those two lines meet is where the specific complex number is.
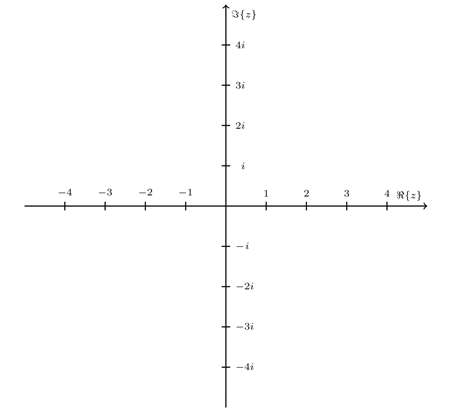
If you are looking at a print-out of this, feel free to try your hand at locating a few complex numbers on the complex plane with a pen or pencil. Don't worry about being precise; the point of the exercise is to understand the general idea.
It's not a rule, and it's certainly not written in stone, but mathematicians generally like to use x and y for purely real numbers. Then yi is a purely imaginary number and x + yi is a complex number.
Mathematicians also like to use a single letter or symbol for anything that they have to write more than once. Even if it's just twice, but you have to admit that some of the things we're talking about here have been mentioned several times. So rather than writing x + yi over and over again, x + yi = z seems almost logical and natural.
And z can still refer to a purely real number (in which case y = 0, and obviously yi = 0 also) or a purely imaginary number (in which case x = 0).
The functions Re and Im come in handy: If z = x + yi, then the real part is Re(z) = x and the imaginary part divided by i is Im(z) = y. There are some very nice and fancy symbols for Re and Im, but depending on your computer's font, you may or may not be able to see them: ℜ and ℑ (if your computer's font doesn't have these symbols, you should be able to see them in Figure 3 above).
Another one that comes in handy is the absolute value function. If −x is a negative number, then abs(−x) = x; for example, abs(−7) = 7. And if x = 0 or a positive number, then abs(x) = x.
It is easy to tell how far a particular purely real number x is from 0. If x is positive, then x is x away from 0. And if x is negative, then x is abs(x) away from 0. Since x = abs(x) when x is positive (or 0), we can just say that abs(x) tells us the distance of x from 0.
Come to think of it, determining the distance of a purely imaginary number yi from 0 is also very easy. As we agree that y is a purely real number, it follows that both y and yi are the same distance away from 0, namely abs(y).
With the right technique, this determination is also easy for a complex number x + yi with nonzero real part and nonzero imaginary part (meaning x ≠ 0, y ≠ 0 either). The right technique is to take advantage of the Pythagorean theorem, which you might remember from high school geometry.
The ancient Greeks did not know about complex numbers, but they did know that in a triangle with a right (90-degree) angle, the longest side (the hypotenuse) is measured by the square root of the sum of the squares of the two other sides. If c is the longest side and a and b are the other two sides, then we have c = √(a2 + b2).
This is relevant to a complex number x + yi, not purely real nor purely imaginary, because we can form a triangle with a right angle by drawing a line from 0 to x, then to x + yi and then back to 0. Here's an illustration for −4 + 3i:
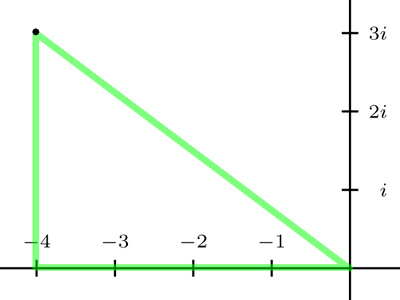
If you prefer, we can also form the triangle by drawing a line from 0 to yi, then to x + yi and then back to 0. Either way we have a triangle with a right angle and the longest side is the distance from 0 to x + yi. Which means that x + yi is √(x2 + y2) away from 0.
And we don't have to worry about either x or y or both being negative, because they'll square to positive numbers anyway. So in our example we have (−4)2 + 32 = 25, and √25 = 5. This means that −4 + 3i is 5 away from 0.
I deliberately chose an example involving integers only, in order to keep things simple; which square integers can be expressed as a sum of two other square integers gets into algebraic number theory, which is very interesting in its own right but is beyond the scope of this page. Already this subsection might seem like a digression from the topic of the Mandelbrot set.
We can also apply this Pythagorean principle to measuring the distance between two complex numbers x + yi and v + wi such that x ≠ v and y ≠ w. Simply compute (x + yi) − (v + wi) or (v + wi) − (x + yi) (doesn't matter which) and then compute the distance of that number from 0.
We're now ready to start putting all this together. We'll start by computing a few steps of the iteration of z2 + c with c = 2i. Obviously (2i)2 = −4, so the first step of the iteration gives us −4 + 2i. Then 12 − 14i, −52 − 334i, −108852 + 34738i.
These numbers are not escaping to positive infinity, but they are getting very far away from 0 very fast, and in a very practical sense, they're growing too large for our computers to handle. We could say that the iteration is escaping to a "directionless" infinity.
We could program the computer to consider that the iteration has escaped to some infinity if either abs(Re(z)) > 2 or abs(Im(z)) > 2, or both, and thus move on to the next point.
Now let's try c = i. Remember that i2 = −1, so the first step of the iteration here gives us −1 + i. Next we have (−1 + i)2 = −2i, so adding i gets us to −i. Take a moment to verify these calculations with the multiplication formula given a few paragraphs earlier.
Remember that negative real numbers have two square roots: one is positive imaginary, the other is negative imaginary. Thus i2 = (−i)2 = −1. Therefore the next step in the iteration brings us back to... −1 + i.
So the iteration bounces back and forth between two distinct values. This is a stable orbit. Pretty much the same thing happens with c = −i.
Can we assume that every point in a straight line between i and −i attains a stable orbit? That is, that if Re(c) = 0 and −1 ≤ Im(c) ≤ 1, then the iteration of z2 + c does not escape to some infinity? That would be a wrong assumption, but let's run with it for now.
If we paint black on the real number line and the imaginary number line those points that don't escape to infinity, using the assumption mentioned just now, we get a cross:
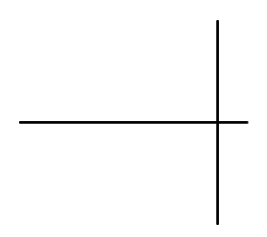
Not the most interesting thing, but we haven't looked at complex values of c yet. If we were to make assumptions about each vertical line, like we did with Re(c) = 0, it would still take us a long time to go through. So at this point, it would be perfectly reasonable to guess that the diagram we've been working on should look something like this:

But that's based on a few faulty assumptions, the first one being that all purely imaginary c between i and −i attain stable orbits under the iteration. It's not hard to find c to prove that assumption wrong. For example, c = 9i/10, which takes less than ten iterations to start getting far away from 0.
As humans, we can grow impatient at having to do a bunch of calculations, whereas a computer will not complain about the drudgery of a million calculations, provided it has been properly programmed.
To produce the diagram we've been talking about on a screen with HD 1080P resolution requires looking at more than two million distinct values of c, which means at least two million calculations: just one or two for the rapidly escaping points, and as many as the iteration maximum we've set for the stable orbit points. And so, with the proper programming, we should obtain the following diagram:

To have some semblance of mathematical rigor, I should explain that this diagram shows us the Mandelbrot set but is not actually the set. The Mandelbrot set is the set of all points c that attain a stable orbit under the iteration of the function z2 + c initialized with z = 0 (or c).
Although Figure 6 is way more correct than Figure 5, it would lead us to believe that the various little dots surrounding the main mass of points c are not pathwise connected, but they in fact are. Well, at least the ones that can be seen in Figure 6, I'll delve a little bit more into this question a little later on.
But perhaps now is the proper time to explain the flip. Mandelbrot and his colleagues were studying the iteration of z2 − c rather than z2 + c. But all this does is flip the diagram along the imaginary number axis (which is vertical).
Back in 1995, I copied a simple program off a book. I made a few modifications to the program, some which were absolutely necessary for the program to run on the setup available to me at the time, some were purely stylistic and affecting only the appearance of the source code, and a few were to optimize performance.
To show you how fast computers have gotten in the past twenty years, I'm going to tell you about a couple of the performance optimizations. One of those modifications turned out to be utterly unnecessary for today's computers.
I'm fairly certain the program as written in the book did not take advantage of the symmetry of the Mandelbrot set (e.g., if you know that c = a + bi escapes, then you also know that c = a − bi does too). Presumably that was to allow readers to modify the program to draw an area of the Mandelbrot set diagram that might not necessarily be symmetrical.
So I modified the program to take advantage of the symmetry and thus cut the calculation time in half. Thus the program worked in two vertical lines from left to right, with one line starting at the top of the screen and the other at the bottom, and meeting each other in the middle of the screen.
I also added a line to the program instructing the computer to place a white or red dot (I don't remember which color it was) at the point c before doing the iterative calculations and coloring the point according to those calculations. The effect of this was to cause two white or red dots to move across the screen as the computer drew the Mandelbrot set.
This way, as the computer moved through several consecutive stable orbit points, you had some indication that it was doing something, that it hadn't crashed. Well, in 2005, I dug out the program with my modifications and ran it: the computer drew the Mandelbrot set so fast the moving dots were completely unnecessary, I couldn't even see them.
While I can pat myself on the back for my ingenuity on the modifications, the fact is that it would have taken a lot of work to turn the program into a full-fledged fractal program. I briefly considered working on just such a program, but fortunately I became aware of FractInt before I took on that massive endeavor.
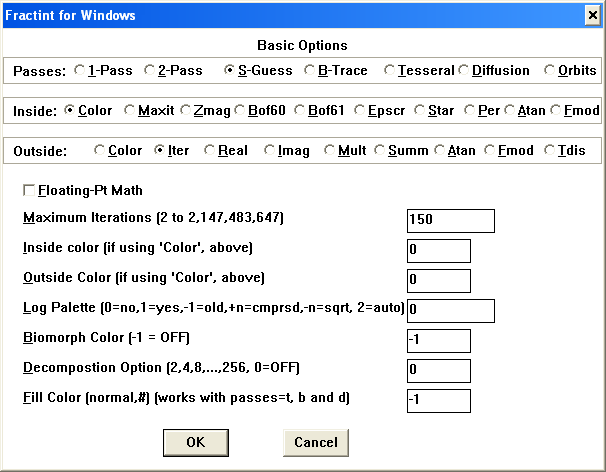 The WinFract Basic Options dialog box, accessible through Fractals > Basic Options...
The WinFract Basic Options dialog box, accessible through Fractals > Basic Options...I'm not sure at what point I became aware of FractInt. It was a DOS program that was already available in 1995, and which back then could be obtained by sending a check or money order (for a modest shipping and handling fee) to some address I don't remember, and receiving a 3.5" floppy disk to install the program. They would also send an iron-on so you could put a fractal on a T-shirt.
If I still had that floppy disk, its only value would be as a collectible. Nowadays you can just download FractInt (and WinFract) from the Internet like just about every other program. Just be sure to get it straight from fractint.org (the link should open in a new window or tab) so it comes by itself, not bundled with any obnoxious adware or whatever.
As late as 2010 I got the impression that DOS was still a fundamental structure underlying the Windows operating system. I don't think that's the case anymore with Windows 8.1, though the DOS command line is still available. DOS is essentially a relic, as most of its users have moved on to Windows.
WinFract has all the functionality of FractInt, but with all graphical user interface niceties we have come to take for granted in Windows. As much as I like keyboard shortcuts, I've really come to appreciate being able to use the mouse to point at things on the screen.
In regards to fractals, the mouse is especially handy for telling the program where to zoom in. As it turns out, FractInt has had mouse support from fairly early on. Though I do wish WinFract had more keyboard shortcuts.
The big downside to FractInt and WinFract right now (as of 2016) is that neither of them can run in Windows 7, 8 or 10. It needs to be ported to work with 64-bit processors. Even a simplistic recompile that does not necessarily take advantage of the computer's 64-bit capabilities would be a major undertaking, and is probably outside the skill set of the vast majority of people reading this page.
Fortunately for me, I still have access to some older computers running Windows XP. WinFract runs like a dream on one of those, with speeds that would have astounded me in 1995. Most of the images on this page were generated by WinFract running on that computer. Some of them I touched up in Adobe Photoshop Elements 8 running on my Windows 8.1 computer at home.
I don't know about Windows 7 or 10, but I can tell you for a fact that ChaosPro 4.0 does run in Windows 8.1. And it's freeware, just like FractInt and WinFract. But be sure to get it straight from chaospro.de (the link should open in a new window or tab).
It seems that ChaosPro can do everything that FractInt and WinFract can, and a lot more. But ChaosPro is geared more towards 3-dimensional images that you can move on a 2-dimensional screen. Along with all that power comes a very steep learning curve. It took me several minutes to figure out how to make it just draw the standard Mandelbrot set (which is the default fractal on both FractInt and WinFract).
To draw the Mandelbrot set in ChaosPro, the menu command is File > Fractal > Escape Time, or you can use the keyboard shortcut Ctrl-4. I have yet to figure out how to get it to draw the other 2-dimensional fractals that I know FractInt is capable of and which I believe ChaosPro can do as well.
FractInt has been ported to Linux, and I think also to Mac OS X. There's also FRAX for iPhones and iPads; it is said to be the best fractal program for touchscreen devices. I am also aware of fractal apps for other smartphones, but I would be wary of whether they perform the calculations on your device or send them off to a server and then retrieve the results; look for phrases like "data transfer rates may apply."
Even if you don't remember, you've surely seen a few different color variations for the Mandelbrot set. Not even the correspondence of black to points that attain a stable orbit is standard as much as that may seem to be the case: you may have seen illustrations in which the stable orbit points are colored blue or red or some other color.

I personally prefer black for the stable orbit points, and I think lots of other people do, too. The boundary between those points and the points that escape to infinity, that's what mathematicians care about. For that purpose, black and white is sufficient, and for mathematicians, sufficient is perfect.
But for computer graphics enthusiasts, black and white does not even begin to show off the capabilities of their screens. Thus they have come up with various schemes to illustrate the Mandelbrot set with a greater variety of colors.
One option to bring in more colors is to color the escaping points according to how fast the escape is. Points that escape very quickly, or immediately, like c = 2, could be colored a dark blue. Points that escape slowly, like c = 0.251 (the iteration takes 96 steps to go above 2), could be colored white (remember, for these points, you want a light color to constrast with the black of the stable orbit points).
Now, some people complain that this produces some ugly banding. There are ways to still use the speed of escape to determine the color yet create smooth gradients among the escaping points. I don't care much for this one way or the other, I am of the opinion that as long as the coloring algorithm does not distract from the main interest (the demarcation between the stable orbit points and the escaping points), it is quite unimportant.
The way FractInt and WinFract do colors is by means of "color maps." default.map is the default color map, which is a fairly straightforward use of the colors that were available on the old VGA displays.
Both FractInt and WinFract come with about twenty other color maps besides the default map, plus it looks like you can also design your own color maps. But in my experience, other color maps cause glitches with saving images, so you may have to use the Alt-PrintScreen kludge.
There are more wonders of the Mandelbrot set to see when we zoom in. WinFract has the Zoom In box selected by default: you simply click and drag to make a rectangle (which you can reposition if you want) and hit Enter.
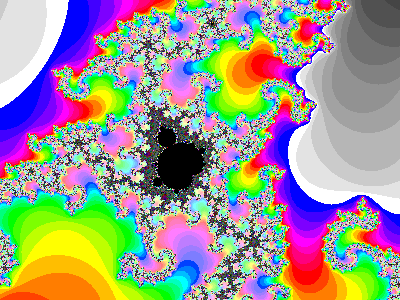
Depending on the program and how close you zoom in, you might need to adjust the number of iterations. If things start looking blocky, fuzzy or just generally not sharp, the number of iterations might need to be increased.
The WinFract default is a maximum of 150 iterations per point, which is just fine for a drawing of the whole set on an HD screen, but can be problematic even for modest zooms.
To increase the iteration maximum, the menu command is Fractals > Basic Options... This brings up a dialog box in which you can type in a number for "Maximum Iterations." A new value of 1,000 might be sufficient if you have only zoomed in a couple of times.
The maximum number of maximum iterations per point in WinFract is 2,147,483,647. This number was not pulled out of a hat: it is the largest number a computer can hold in memory as a signed 32-bit integer. Presumably if WinFract was ported for 64-bit Windows this maximum could be boosted to 9,223,372,036,854,775,807.
However, even with our faster computers, the maximum iteration maximum is probably overkill if you're not looking to test how close you can zoom in. I suggest raising the maximum iteration maximum in steps of 1,000 or 10,000 as you zoom in.

As you zoom in, you should notice small copies of the whole big shape. And these copies are in turn surrounded by yet smaller copies of the whole shape. Mathematicians say the shape is "self-similar." Self-similarity is one of the defining characteristics of a fractal.
Long before computers made it practical to draw fractals like the Mandelbrot set, a few mathematicians were able to determine certain important facts about these fractals, but many questions remain. For instance, are all the little copies of the overall shape pathwise connected?
To state this in a rigorous manner, we can say that from any point c such that the iteration of z2 + c does not escape to infinity, to any other point with the same property, it is possible to draw a path to connect those two points such that all points on the path also have that property. Or at least, we believe that it is possible to draw such a path.
For example, chart a path from 0 to i without leaving the Mandelbrot set. As we already saw, 9i/10 is not in the Mandelbrot set, and neither are a lot of points surrounding it, so our path would have to avoid it. The final stretch of the path is especially tricky, and you'd probably want the diagram displayed in black and white in order to see the path.
In many cases, the connecting paths will be very narrow and require a lot more iteration to reveal them than your computer is capable of. Also, many of those connecting paths can be incredibly long and tortuous.

There are also some smooth, straight line paths between little copies, such as those along the real axis. In the following image, you can see the little copy at c = −1.75, and maybe you can also see a couple other smaller copies lined up horizontally:

Can the perimeter of the Mandelbrot set can be measured, like the perimeter of a square or a circle or an oval? If a square has a side measuring x, then obviously the perimeter is just 4x.
The perimeter of a circle (its circumference) can be calculated with a formula that involves π, which is approximately 3.14159. It's a little more involved to calculate the circumference of the oval shown in Figure 5, but it's still quite doable.
Well, for the Mandelbrot set, we can't calculate its perimeter, but we know what it is: it is positive infinity! Though I suppose that assumes the whole set is pathwise connected.
I suppose this is a place as good as any to take a break. We can pick it up later with the topic of Julia sets and how they relate to the Mandelbrot set.